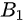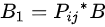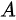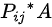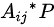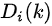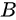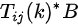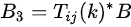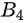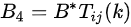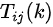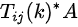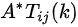初等矩阵是指由单位矩阵经过三种矩阵初等变换得到的矩阵。初等矩阵的模样可以写成一个三阶或者四阶的单位矩阵，首先：初等矩阵都可逆，其次，初等矩阵的逆矩阵其实是一个同类型的初等矩阵（可看作逆变换）。例如，交换矩阵中某两行（列）的位置；用一个非零常数k乘以矩阵的某一行（列）；将矩阵的某一行（列）乘以常数k后加到另一行（列）上去。若某初等矩阵左乘矩阵A，则初等矩阵会将原先施加到单位矩阵E上的变换，按照同种形式施加到矩阵A之上。或者说，想对矩阵A做变换，但是不是直接对矩阵A去做处理，而是通过一种间接方式去实现。
初等行变换不影响线性方程组的解，也可用于高斯消元法，用于逐渐将系数矩阵化为标准形。初等行变换不改变矩阵的核（故不改变解集），但改变了矩阵的像。反过来，初等列变换没有改变像却改变了核。
初等矩阵
Elementary matrix
线性代数
基本矩阵
单位矩阵
数学
（1）交换矩阵中某两行（列）的位置1；
（2）用一个非零常数乘以矩阵的某一行；
（3）将矩阵的某一行（列）乘以常数k后加到另一行上去。
三类初等矩阵都是可逆矩阵，即异阵。
三类初等矩阵的值是：
（1）：-1
（2）：k
（3）：1
1、单位矩阵第i,j两行互换得到的方阵为
说明：任意矩阵
2、单位矩阵第i行乘以常数k得到初等方阵
说明：任意矩阵
3、将单位矩阵的第i行的k倍加到第j行得到初等方阵
说明：任意矩阵
（1）在解线性方程组中的应用
初等行变换不影响线性方程组的解，也可用于高斯消元法，用于逐渐将系数矩阵化为标准形。初等行变换不改变矩阵的核（故不改变解集），但改变了矩阵的像。反过来，初等列变换没有改变像却改变了核。
（2）用于求解一个矩阵的逆矩阵
有的时候，当矩阵的阶数比较高的时候，使用其行列式的值和伴随矩阵求解其逆矩阵会产生较大的计算量。这时，通常使用将原矩阵和相同行数（也等于列数）的单位矩阵并排，再使用初等变换的方法将这个并排矩阵的左边化为单位矩阵，这时，右边的矩阵即为原矩阵的逆矩阵。