行最简形矩阵(Row simplest form matrix),线性代数名词,是指线性代数中的某一类特定形式的矩阵。
矩阵在经过初等行变换化为最简形矩阵后,再经过初等列变换,变化为标准形矩阵,因此,任一矩阵可经过有限次初等变换化成标准形矩阵。

行最简形矩阵(Row simplest form matrix),线性代数名词,是指线性代数中的某一类特定形式的矩阵。
矩阵在经过初等行变换化为最简形矩阵后,再经过初等列变换,变化为标准形矩阵,因此,任一矩阵可经过有限次初等变换化成标准形矩阵。
行最简形矩阵
Row simplest form matrix
名词
线性代数
在阶梯形矩阵中,若非零行的第一个非零元素全是1,且非零行的第一个元素1所在列的其余元素全为零,就称该矩阵为行最简形矩阵。
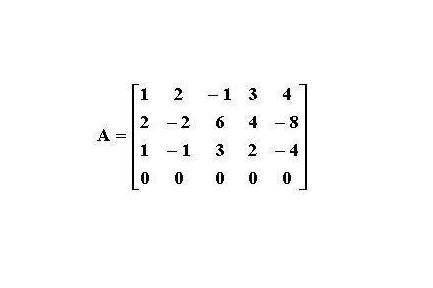
例如矩阵:
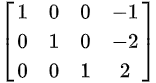
下列三种变换称为矩阵的行初等变换:
(1)对调两行;
(2)以非零数k乘以某一行的所有元素;
(3)把某一行所有元素的k倍加到另一行对应元素上去。
将定义中的“行”换成“列”,即得到矩阵的初等列变换的定义1。矩阵的初等行变换与矩阵的初等列变换,统称为矩阵的初等变换。
有如下定理成立:
任一矩阵可经过有限次初等行变换化成阶梯形矩阵;
任一矩阵可经过有限次初等行变换化成行最简形矩阵;
矩阵在经过初等行变换化为最简形矩阵后,再经过初等列变换,变化为标准形矩阵,因此,任一矩阵可经过有限次初等变换化成标准形矩阵。
行最简形矩阵是由方程组唯一确定的,行阶梯形矩阵的行数也是由方程组唯一确定的。